Earlier in the series we saw that the purpose of monitoring progress on a task is simply to ensure that it performing according to expectations. These are set by the plan, specifically the baseline that represents the original forecast for the schedule, the cost, the use of resource and the delivery of quality. Where performance deviates from those expectations we need to identify and understand the causes. We saw in an earlier blog (link) that these causes are confined to a handful of broad areas, involving the productivity of the resources, their rate of attendance, and the punctuality of the start. Of course these can each be analysed to reveal a variety of sub-causes which will need to be addressed. Also, the deviations could also be due to an expansion or contraction of the scope which we will handle at the end of this post.
It is important that monitoring is performed at the lowest level available in the WBS, that relating to tasks or activities. This is where the data is most precise and the focus most clear. Individual task performance may itself not be of much interest to stakeholders who are probably after similar reporting at higher levels of the WBS. However, the accuracy available there is achieved by aggregating the results recorded for their constituent individual task behavior. Hence we cannot do without a careful analysis of task behavior. In what follows, we introduce measures designed to reflect the degree to which the broad causes mentioned above are responsible for any deviations from the baseline.
Consider a case where it is reported that we have achieved 30% of the actual progress on a task, measured in some appropriate way. We shall call this the ‘Actual Progress’ or ‘AP’. To be more precise this is the Actual Progress (to this date) from the point of Actual Start. Suppose further that we know from the baseline data that we ought to have achieved 50% completion by now – that is had everything gone according to plan. We shall call this figure the Baseline Progress or BP, which can also be described as the Planned Progress (to this date) from the point of Planned Start. A natural way of quantifying this situation is to form the expression for what we shall call the (overall) Schedule Factor SF by means of the expression 

or

Clearly a value of 1 for this ratio would indicate that the task is performing according to expectations while if it rises above 1 performance is better than expected. In the case we are considering, the value computes to 30%/50% or 0.6 which indicates that problems exist.
Defining a Punctuality Factor ratio
Let us first examine the case where the entire reported progress deficit is due to the late start. This implies that there are no problems in the implementation of the task itself once it has got going. Put another way, ignoring the late start, 30% is precisely the progress we should have expected at this stage. Let us call this the (currently) Expected Progress (EP), that is, the progress currently expected ignoring the effects of an early or late start. Alternatively we could say that the EP is the Planned Progress (to this date) from the point of Actual Start. The situation would appear as shown in figure 1.
 | ||||
| ||||
It seems reasonable then to describe the effect of the late start, a value we shall call the ‘punctuality
factor’ (PF) as again giving a value of 0.6 which provides a full account of the overall schedule deficit we saw in equation (1) since we are assuming no problems were found in the implementation of the task.
Defining a Duration Factor Ratio
Note the difference between ‘Actual Progress’ and ‘Expected Progress’. The former represents what we have actually achieved while the latter reflects the performance that should have been achieved, ignoring variations in start times. In the case we are considering they are numerically equal because we are assuming that all of the delays can be attributed to the late start. This suggests that a ratio describing the performance of the task itself, expressed in terms of the health of its duration prospects relative to the original baseline forecast, sh should be

Again, this compares, to this date, the Actual Progress compared to the Planned Progress, both measured from the point of the Actual Start and in this case gives a value of 1 indicating that all is proceeding according to plan on the task itself, late start notwithstanding. Now let us suppose that the delayed start does not fully explain the deficit and that problems were found in the implementation of the task. Consider the case below where Actual Progress is only 20%, and since the Expected Progress is 30%, on current trends the task duration itself will be extended and add further delay to that expected due to the late start.
 |
| Figure 2: Schedule deficit due to delay and productivity loss |
Here we find the DF equal to or 20%/30% = 2/3 indicating that if current trends continue, an extension in duration would result. From our definitions of SF, DF and PF it is clear that 

so that SF = 2/3 * 0.6 = 0.4
Equations like (3) reveal the entire point of this analysis. It is one thing to know that the task if falling behind (0.4 being a very low ratio compared to 1), but quite another to understand its underlying causes. The decomposition of SF into its two constituents provides the means for understanding their relative contributions to this poor state of overall schedule health. Specifically, overall schedule performance is seen to consist of two effects, the duration and punctuality performance. This makes sense. How well a swimmer performs relative to the overall time expected in a race depends upon both the quality of the start at the gun and of performance across the pool. This sort of analysis provides swimming coaches and project managers with valuable insights into the causes of variations from the expected.
Note that from equation (3) we can see that the duration and punctuality factors can compensate for each other. For example an SF value which would otherwise suffer from a late start of say PF = ¾ could be rescued by a task performing better than expected by a factor of 4/3, restoring it to a value of 1 or par. On the other hand, these two effects can re-enforce each other. An early starting task (say PF = 4/3) along with this good task progress performance would provide a very healthy overall schedule factor SF of 4/3 * 4/3 = 16/9 = 1.77.
Defining Attendance and Productivity ratios
In a very similar way, we can break open the Duration Factor measure in an effort to understand the factors that influence it. Clearly one such factor would be the degree to which resources are working on the task relative to what was expected in the baseline. Following our definition of DF, let us define an Attendance Factor ratio as

where Actual Effort reflects the actual hours recorded and Expected Effort those that should have been recorded (if all human resources scheduled in the baseline plan had shown up for work) both since the point of Actual Start.
Let us suppose that this ratio is found to be 0.8, implying that there was a 20% loss of resources. Assuming that the size or scope of the task has not changed (a factor we shall treat later), any departures of DF from unity not explained by this absenteeism can only be attributed a drop in productivity – something we shall call the ‘Efficiency Factor’, (EF). Consider the ratio

From equations (2) and (4) it is evident that

which can also be written as

Now we know that the Progress/Effort ratio is a measure of productivity or efficiency and so EF can be interpreted as the productivity compared against that expected in the original baseline forecast. It follows that

The dependence of duration on productivity and resource attendance is true for all productive processes. For example, economic output is measured this way. Similarly, a swimmer’s progress across the pool is a function of the productivity of each stroke (distance achieved by each) multiplied by the number of strokes (resources inputs). Of course, as we saw, her overall time (schedule performance factor) would also be affected by any late start compared to other racers. This is confirmed when we combine equations (3) and (5) to produce 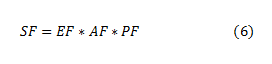
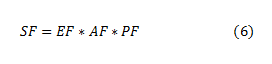
In our example, we therefore have
| SF | EF | AF | PF |
| 0.4 | 0.83 | 0.8 | 0.6 |
In this case the poor schedule performance is due to three factors all performing badly. The task started late, has lost resources and those that have worked have done so at below-par productivity.
Equation (6) therefore illustrates the main constituent factors contributing to schedule performance and allows us to see the relative responsibilities that each has to any divergence from the expected value of 1.
Relationship with Earned Value
Readers familiar with Earned Value Analysis (EVA) methods will see some similarities in the process described above. The obvious differences lie in our focus on work hours rather than costs which dominate the EVA approach. We also introduce additional factors such as DF, PF and AF for which there are no equivalents in EVA, although these could be very easily introduced as discussed in our paper delivered to the Australian Institute of Project Management Conference, Canberra, October 2008 entitled ‘Towards a Complete Earned Value Analysis’. Where the two systems overlap, it is clear that our value for EF is analogous to the CPI (cost performance index) in EVA, representing a cost efficiency factor and SF is analogous to SPI (schedule performance index), representing a time efficiency measure.
The Effects of Scope Change
One of the additional factors introduced in our paper related to the effects of scope change. It is clearly possible to be falling behind on progress relative to a scope that has grown since the baseline was set, without being formally recognized in that baseline. In a treatment slightly different from the one we gave in that paper, we could introduce a measure M to reflect the magnitude of the work to be completed according to the baseline. This could be measured in relevant units depending upon the nature of the task. If M’ is the new size of the task, resulting from a change in scope, we could introduce the factor KF = M/M’ to reflect this. We can now modify the SF value in (6) to become
Thus if M is greater than M’, reflecting a situation of scope creep or some other mechanism for its increase, KF is smaller than 1 and SF is further reduced.


No comments:
Post a Comment